10)
In general, the sum of the inner angles of a polygon is given by the formula below
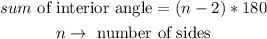
Therefore, in our case, since we are dealing with a polygon of seven sides,
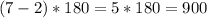
Then,
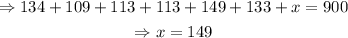
Thus, the answer to question 10 is x=149°.
11)
Using the formula for the sum of the inner angles of a polygon used in part 10),
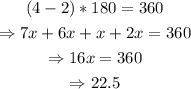
Therefore, the answer to question 11) is x=22.5