Question

3 men and 3 woman line up at a checkout counter in the store. find the probability that the first person in line is a woman in the line alternates by gender.

Answer 1

Probability first is a woman: P( 1W)

`\begin{gathered} P(1W)=\frac{\#\text{women}}{\#persons\text{ line up}} \\ \\ P(1W)=(3)/(6)=(1)/(2)=0.5 \end{gathered}`

The probability that the first person in the line is a woman is 1/2 or 0.5 or 50%.

To find the probability of the alternate by gender:

Find the probability that the second person is a man P(2M). Knowing that the first person is a woman.

In this case the number of persons line up is 5 (as you don't need to count the first person):

`\begin{gathered} P(2M)=\frac{\#\text{men}}{\#persons\text{ line up left}} \\ \\ P(2M)=(3)/(5)=0.6 \end{gathered}`

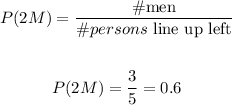
find the probability that the third person is a woman P(3W):

`\begin{gathered} P(3W)=\frac{\#\text{women left}}{\#persons\text{ line up left }} \\ \\ P(3W)=(2)/(4)=(1)/(2)=0.5 \end{gathered}`

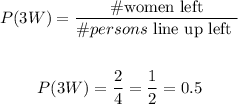
Find the probability that the fourth person is a man:

`\begin{gathered} P(4M)=\frac{\#\text{men left}}{\#persons\text{ line up left}} \\ \\ P(4M)=(2)/(3)=0.6\bar{6} \end{gathered}`

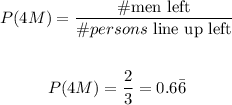
find the probability that the fifth person is a woman:

`\begin{gathered} P(5W)=\frac{\#\text{women left}}{\#persons\text{ line up left}} \\ \\ P(5W)=(1)/(2)=0.5 \end{gathered}`

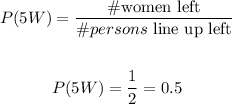
Find the probability that the sixth person is a man:

`\begin{gathered} P(6M)=\frac{\#\text{man left}}{\#persons\text{ line up left}} \\ \\ P(6M)=(1)/(1)=1 \end{gathered}`

Then, multiply all six probabilities:

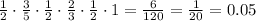
`(1)/(2)\cdot(3)/(5)\cdot(1)/(2)\cdot(2)/(3)\cdot(1)/(2)\cdot1=(6)/(120)=(1)/(20)=0.05`Then, the probbility taht the first person is a woman and then alternate by gender is 1/20 or 0.05 or 5%