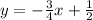Answer:
Step-by-step explanation:
A general equation for a line in the slope-intercept form is y = mx + b.
Given the points (-6, 5) and (-2, 2), we can substitute the first point in the equation:
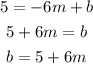
Now, we can substitute the second point in the equation and use the relation for "b" found above:
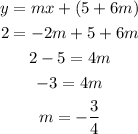
Since b = 5 + 6m, we can now find b:
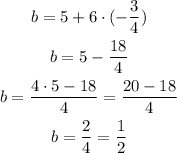
Thus, the equation of the line is: