Given:
The force of repulsion between the electrons is,
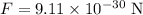
The charge of each electron is,
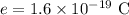
To find:
The distance between the electrons
Step-by-step explanation:
The force between two electrons at a distance 'r' is,
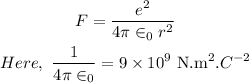
Substituting the values, we get,
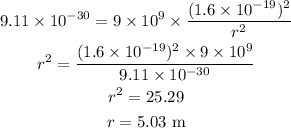
Hence, the distance between the electrons is 5.03 m.