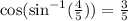Solution:
We want to solve the following expression:
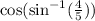
Let us denote by epsilon the argument of cosine function:
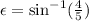
now, applying the sine function to both sides of the equation, we get:
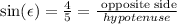
this equation can be represented in a right triangle like this:
now, we want to find:
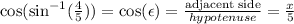
Note that we just need to find x to solve this problem. Then, to find x, we can apply the pythagorean theorem:
According to the right triangle, we get:
![x=\sqrt[]{5^2-4^2}\text{ =3}](https://img.qammunity.org/2023/formulas/mathematics/college/a9db96p0o1lk96fg3vhophtjmpbdxk0usf.png)
thus, we can conclude that:
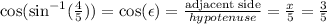
So that, the correct answer is: