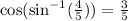Question

How do I use a sketch to find the exact value of the problem in the image?

Answer 1

We want to solve the following expression:

`\cos (\sin ^(-1)((4)/(5)))`

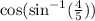
Let us denote by epsilon the argument of cosine function:

`\epsilon=\sin ^(-1)((4)/(5))`

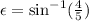
now, applying the sine function to both sides of the equation, we get:

`\sin (\epsilon)=(4)/(5)=\frac{\text{ opposite side}}{hypotenuse}`

this equation can be represented in a right triangle like this:

now, we want to find:

`\cos (\sin ^(-1)((4)/(5)))=\cos (\epsilon)=\frac{\text{adjacent side}}{hypotenuse}=(x)/(5)`

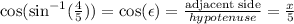
Note that we just need to find x to solve this problem. Then, to find x, we can apply the pythagorean theorem:

According to the right triangle, we get:

`x=\sqrt[]{5^2-4^2}\text{ =3}`

thus, we can conclude that:

`\cos (\sin ^(-1)((4)/(5)))=\cos (\epsilon)=\frac{\text{adjacent side}}{hypotenuse}=(x)/(5)=(3)/(5)`

So that, the correct answer is:

`\cos (\sin ^(-1)((4)/(5)))=(3)/(5)`