Question

If x = 7/4, then the graph of the absolute value function will be __________________ than the line x = -3/2.closer to the y-axiscloser to the x-axisfurther from the y-axisfurther from the x-axis

Answer 1

Given: A value of x as-

`x=(7)/(4)`

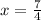
Required: To determine the position of the given x value with respect to the line-

`x=-(3)/(2)`

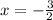
Explanation: A function's absolute value always gives a positive value.

So for the given x value, we have

`\begin{gathered} x=(7)/(4) \\ \Rightarrow\lvert{x}\rvert=(7)/(4) \end{gathered}`

Since the given x is a positive real number, it will not be affected by the modulus function.

Now, x=a is a vertical line parallel to the y-axis and at 'a' distance from it.

Therefore the graph of both lines are

The red graph represents the graph of x=7/4 while the green line represents the line x=-3/2.

The distance of green line from y-axis is-

`x=-1.5`

Similarly red line is at -

`x=1.75`

Since,

`\lvert{-1.5}\rvert<\lvert{1.75}\rvert`

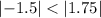
We see that line x=7/4 is further from the y-axis than line x=-3/2.

Final Answer: Option C is correct.