Please help me I don't think my answer is correct

Question

asked May 5, 2023 171k views

1 Answer

Chaviva · Answer 1 · 2023-05-11T17:19:44+0000

To find the derivatives we have to use the following property:

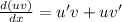
$(d(uv))/(dx)=u^(\prime)v+uv^(\prime)$

Then the first derivative will be:

$y\text{ = 2xe}^(-x)$

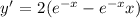
$y^(\prime)\text{ = }2\mleft(e^(-x)-e^(-x)x\mright)$

Now to find the second derivative we have to use the same derivative property with the part "-xe^-x. Thus:

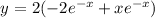
$y^(\doubleprime)=2(-2e^(-x)+xe^(-x))$

Now we have to equal the equation to zero:

$e^(-x)(x-2)=0_{}$

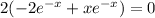
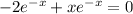
The first solution will be:

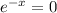
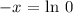
$-x\text{ = ln 0}$

ln 0 is undefined, so this answer is impossible.

The second solution will be:

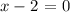
$x-2\text{ = 0}$

$x\text{ = 2}$

Answer: x = 2.