Question

Please help me I don't think my answer is correct

Answer 1

To find the derivatives we have to use the following property:

`(d(uv))/(dx)=u^(\prime)v+uv^(\prime)`

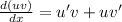
Then the first derivative will be:

`y\text{ = 2xe}^(-x)`

`y^(\prime)\text{ = }2\mleft(e^(-x)-e^(-x)x\mright)`

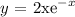
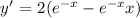
Now to find the second derivative we have to use the same derivative property with the part "-xe^-x. Thus:

`y^(\doubleprime)=2(-2e^(-x)+xe^(-x))`

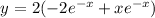
Now we have to equal the equation to zero:

`2(-2e^(-x)+xe^(-x))=0`

`-2e^(-x)+xe^(-x)=0`

`e^(-x)(x-2)=0_{}`

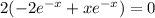
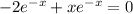
The first solution will be:

`e^(-x)=0`

`-x\text{ = ln 0}`

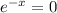
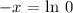
ln 0 is undefined, so this answer is impossible.

The second solution will be:

`x-2\text{ = 0}`

`x\text{ = 2}`

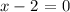
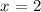
Answer: x = 2.