Question

Can you help me solve using the elimination method:x + 2y = -13x - y +4z = 17-4x + 2y - 3z = -30

Answer 1

we subtract the first equation from the third to eliminate y

`\begin{gathered} x+2y+0z=-1 \\ -4x+2y-3z=-30 \\ ---------------- \\ 5x+0y+3z=29 \end{gathered}`

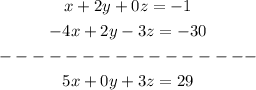
we multiply the second equation with 2 and sum it to the third, to eliminate y too

`\begin{gathered} 6x-2y+8z=34 \\ -4x+2y-3z=-30 \\ ---------------- \\ 2x+0y+5z=4 \end{gathered}`

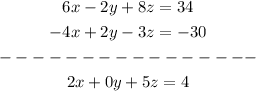
the new equations are the fourth and fifth respectively

Now we will eliminate Z from these two equations

we multiply the fourth equation with 5/3

`\begin{gathered} 5x((5)/(3))+3z((5)/(3))=29((5)/(3)) \\ (25)/(3)x+5z=(145)/(3) \end{gathered}`

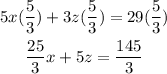
We can name this the sixth equation but it is the same what the fourth

we subtract the sixth equation from the fifth to eliminate z

`\begin{gathered} (25)/(3)x+5z=(145)/(3) \\ 2x+5z=4 \\ ------------ \\ (19)/(3)x+0z=(133)/(3) \end{gathered}`

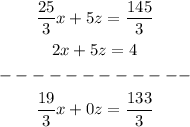
now we can solve X and replace in the other equations to find Y and Z

`\begin{gathered} (19)/(3)x=(133)/(3) \\ x=(133*3)/(19*3) \\ x=7 \end{gathered}`

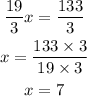
replace x=7 on the fiste equation to find Y

`\begin{gathered} (7)+2y=-1 \\ 2y=-1-7 \\ y=(-8)/(2) \\ y=-4 \end{gathered}`

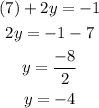
replace y=-4 and x=7 on the second equation to find Z

`\begin{gathered} 3(7)-(-4)+4z=17 \\ 21+4+4z=17 \\ 4z=17-21-4 \\ z=(-8)/(4) \\ z=-2 \end{gathered}`

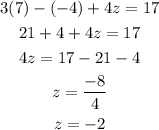
you can check replacing the values ​​in any equation and the equality must be satisfied