we subtract the first equation from the third to eliminate y
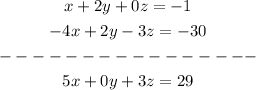
we multiply the second equation with 2 and sum it to the third, to eliminate y too
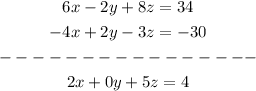
the new equations are the fourth and fifth respectively
Now we will eliminate Z from these two equations
we multiply the fourth equation with 5/3
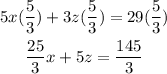
We can name this the sixth equation but it is the same what the fourth
we subtract the sixth equation from the fifth to eliminate z
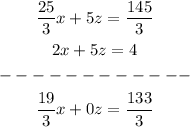
now we can solve X and replace in the other equations to find Y and Z
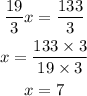
replace x=7 on the fiste equation to find Y
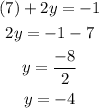
replace y=-4 and x=7 on the second equation to find Z
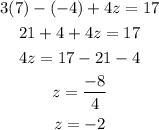
you can check replacing the values in any equation and the equality must be satisfied