Answer:
L = 10.037
W = 2.291
LW = 23..........Equation 1
L = 7W - 6.......Equation 2
*Substitute the value of L to the first equation to solve for W
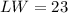
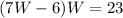
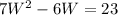
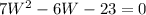
Through quadratic formula, we can get:
![W=\frac{-(-6)\pm\sqrt[]{(-6)^2-4(7)(-23)}}{2(7)}](https://img.qammunity.org/2023/formulas/mathematics/college/1am34d20ou118prs0h9s09slvrxrb8goph.png)
![W=\frac{6\pm2\sqrt[]{170}}{14}](https://img.qammunity.org/2023/formulas/mathematics/college/mq5a3ijp8low3enrhx04d8fvv9wlsceu2d.png)
![W=\frac{3\pm\sqrt[]{170}}{7}](https://img.qammunity.org/2023/formulas/mathematics/college/lgj6z8m92hpknk5vqoxxthnr20vh4a1mdp.png)
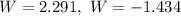
*Since we cannot have a negative value for the dimensions, we will consider 2.291.
Going back to the second equation, substitute the value of W to solve for L.
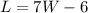
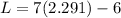
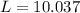
The length of the garden should be 10.037 feet, and the width should be 2.291 feet.