Question

The zeros of a quadratic function are (-2,0) and (8,0). What is a possible vertex of the function? A. (3,0)B. (3,-1)C. (6,0)D. (6,-1)

Answer 1

B(3,-1)

Step-by-step explanation

`y=ax^2+bx+c`

Step 1

Point 1

(-2,0)

replace

`\begin{gathered} y=ax^2+bx+c \\ 0=a(-2)^2+b(-2)+c \\ 0=4a-2b+c \\ 2b-4a=c\rightarrow equation\text{ (1)} \end{gathered}`

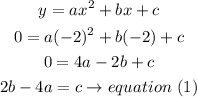
Point 2

(8,0)

`\begin{gathered} y=ax^2+bx+c \\ 0=a(8)^2+b(8)+c \\ 0=64a+8b+c\rightarrow equation\text{ (2)} \\ c=-64a-8b \end{gathered}`

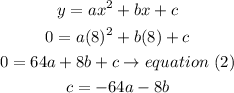
c) c= c, so

`\begin{gathered} 2b-4a=-64a-8b \\ -4a+64a=-8b-2b \\ 60a=-10b \\ (60a)/(-10)=(-10b)/(-10) \\ b=-6a \end{gathered}`

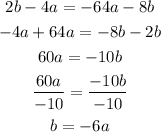
Step 2

when the function is in the form

`y=ax^2+bx+c`

the vertex is given by

`(-(b)/(2a),f(-(b)/(2a))`

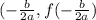
so,replace

`\begin{gathered} -(b)/(2a) \\ -((-6a))/(2a)=(6a)/(2a)=3 \\ \end{gathered}`

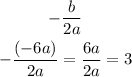
therefore, the component of the vertex is 3

let's check the options

A. (3,0)

B. (3,-1)

we can see that y component of option A is zero , it means (3,0 ) is a zero of the function, but we had already the zeros, therefore, we can discard this options,

in other words,

the answer is

B(3,-1)

I hope this helps you