The Equation of a Hyperbola
If the given coordinates of the vertices and foci have the form (0, a) (0, -a), (0,c), and (0,-c) respectively, then the transverse axis is the y-axis.
The equation of this conic can be written in standard form:
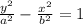
We are given the values of a=2, c = 5. We can find the value of b with the formula:
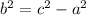
Substituting values:

Thus the equation of the hyperbola is:
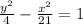
The graph is shown below: