Question

Find the equation of the conic with foci, f and vertices, V.

Answer 1

The Equation of a Hyperbola

If the given coordinates of the vertices and foci have the form (0, a) (0, -a), (0,c), and (0,-c) respectively, then the transverse axis is the y-axis.

The equation of this conic can be written in standard form:

`(y^2)/(a^2)-(x^2)/(b^2)=1`

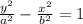
We are given the values of a=2, c = 5. We can find the value of b with the formula:

`b^2=c^2-a^2`

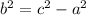
Substituting values:

`\begin{gathered} b=5^2-2^2 \\ \text{Calculating:} \\ b^2=21 \end{gathered}`

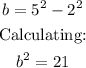
Thus the equation of the hyperbola is:

`(y^2)/(4)-(x^2)/(21)=1`

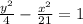
The graph is shown below: