
1) Since we knw towo solutions for this function, we can set a system of linear equations to find the slope m and the y-intercept. Let's use the Substitution Method.

Now that we know the quantity of b, let's plug into one of those equations and solve for x:
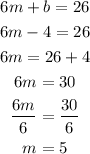
Thus, these are the answers m=5, b=-4