Question

If (6,26) and (-5,29) are two solutions of f(x) =mx+b, find m and b M= b=

Answer 1

`m=5,\:b=-4`

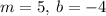
1) Since we knw towo solutions for this function, we can set a system of linear equations to find the slope m and the y-intercept. Let's use the Substitution Method.

`\begin{gathered} f(x)=y \\ y=mx+b \\ (6,26),(-5,-29) \\ 26=6x+b \\ -29=-5x+b \\ \begin{bmatrix}-6m-b=-26 \\ 5m-b=29\end{bmatrix} \\ \\ 26=6m+b\Rightarrow6m+b=26\Rightarrow(6m)/(6)=(26)/(6)-(b)/(6)\Rightarrow m=(26-b)/(6) \\ \\ Substitute: \\ -29=-5((26-b)/(6))+b \\ -29=-(130)/(6)+(5b)/(6)+b \\ -29=-(130)/(6)+(11)/(6)b \\ -(130)/(6)+(11)/(6)b=-29 \\ -(130)/(6)+(11)/(6)b+(130)/(6)=-29+(130)/(6) \\ (11)/(6)b=-(22)/(3) \\ 6\cdot (11)/(6)b=6\left(-(22)/(3)\right) \\ 11b=-44 \\ b=-4 \end{gathered}`

Now that we know the quantity of b, let's plug into one of those equations and solve for x:

`\begin{gathered} 6m+b=26 \\ 6m-4=26 \\ 6m=26+4 \\ 6m=30 \\ (6m)/(6)=(30)/(6) \\ m=5 \end{gathered}`

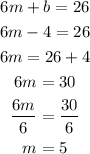
Thus, these are the answers m=5, b=-4