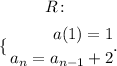Question

Write an explicit rule and recursive rule for each sequence. n 1 2. 3 4 5 1 3 5 7 9 f(1) = d = R= E =

Answer 1

Given:

n = 1 , 2 , 3, 4, 5

f(n) = 1, 3, 5 , 7, 9

Let's find the common differnce,

9 - 7 = 7 -5 = 5 - 3 = 3 - 1 = 2

The common diffrence is 2.

The explicit rule is:

f(n) = 1 + 2(n - 1)

The recursive rule is:

`a_n=a_(n-1)+2_{}`

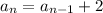
ANSWER:

f(1) = 1

d = 2

E : f(n) = 1 + 2(n - 1)

`\begin{gathered} R\colon_{} \\ \mleft\{\begin{aligned}a(1)=1 \\ a_n=a_(n-1)+2\end{aligned}\mright. \end{gathered}`