Concept :
- To solve this question we will assume the vertices to be P(3,4) and Q(-2,3) and R(x,y)
- All the sides in an equilateral triangle are equal. Therefore PQ = PR = QR, we will find distance between them by using the distance formula
- Then we will equate PR = QR to form an equation in 2 variables [1] after this we will equate PR = PQ and will substitute the value of y from the above equation [1] to get a quadratic equation in one variable, and will solve it! :D
Distance formula =
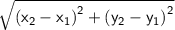
Solution :
Let, the coordinates of vertices of the equilateral triangle be P(3,4) and Q(-2,3) and R(x,y)
Also, PQ = PR = QR
Finding PQ using distance formula,
•
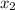 = -2
= -2
•
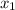 = 3
= 3
•
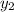 = 3
= 3
•
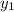 = 4
= 4
Putting the values,
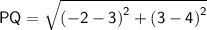
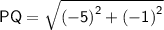
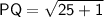
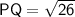
Finding PR using distance formula,
•
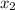 = x
= x
•
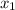 = 3
= 3
•
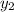 = y
= y
•
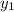 = 4
= 4
Putting the values,
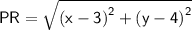
Using (a - b)² = a² + b² - 2ab
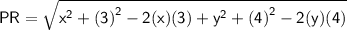
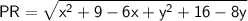
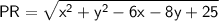
Finding QR using distance formula,
•
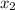 = x
= x
•
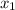 = -2
= -2
•
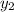 = y
= y
•
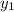 = 3
= 3
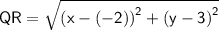
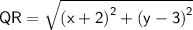
Using (a - b)² = a² + b² - 2ab and (a + b)² = a² + b² + 2ab
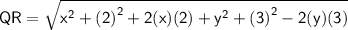
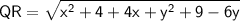
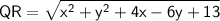
Now, PR = QR
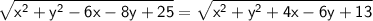
By squaring both sides, the root will get cancel
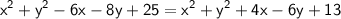
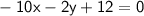
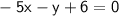
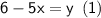
Also PR = PQ
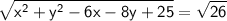
By squaring both sides, the root will get cancel
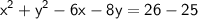
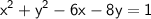
Put value of y from equation (1)
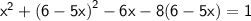
Using (a - b)² = a² + b² - 2ab
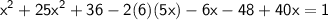
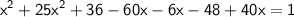
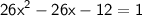
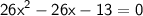
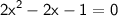
Using quadratic formula to solve the quartic equation,
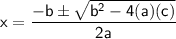
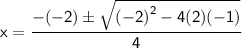
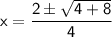
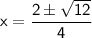
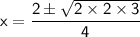
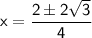
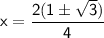
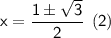
Put value of x in equation (1)
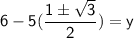
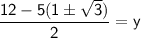
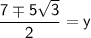
The coordinates of third vertex is
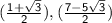 or
or
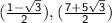
Correct Answer is - Option (b)! :)