The experiment is equivalent to tossing 128 coins at the same time. The probability of a coin landing on heads (yellow) is 1/2. Therefore, if all the coins are fair, after one try, one-half of the coins will land on tails (red). So, only 128/2=64 coins are tossed the second time, and 1/2 of them will land on tails.
After repeating the experiment n times, the expected number of counters that land on yellow at the end of the trial is
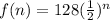
Part B)
Set f(n)=1 and solve for n, as shown below,
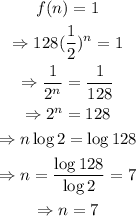
Thus, after 7 trials, exactly one counter will land on yellow.