Answer:
(-3, 4)
Step-by-step explanation:
The centroid is the intersection of the median of a triangle. The medians are segments that go from each vertex to the midpoint of the opposite side.
To find the midpoints of each side, we will use the following
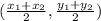
Where (x1, y1) and (x2, y2) are the coordinates of the two vertexes.
So, the midpoint of side AB can be calculated by replacing (x1, y1) by (-6, 8) and (x2, y2) by (-3, 1), then
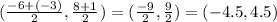
The midpoint of side BC that goes from B(-3, 1) to C(0, 3) is
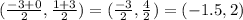
And the midpoint of side AC that goes from A(-6, 8) to C(0, 3) is
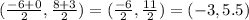
So, we can draw the triangle and the medians as follows:
Therefore, the coordinates of the centroid are (-3, 4)