We need to solve the system of equations:

We can rewrite the first equation as:
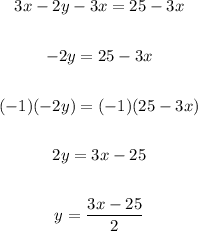
Now, we can replace y with the above expression in the second equation. We obtain:

Now, we use x = 5 to find y:

Therefore, the solution to this system is the ordered pair (5, -5).