Question

Solve the following system using the substitution method. Enter your answer as an ordered pair in the form(x,y) 3x - 2y = 25 5x + 10y = -25

Answer 1

We need to solve the system of equations:

`\begin{gathered} 3x-2y=25 \\ 5x+10y=-25 \end{gathered}`

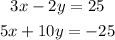
We can rewrite the first equation as:

`\begin{gathered} 3x-2y-3x=25-3x \\ \\ -2y=25-3x \\ \\ (-1)(-2y)=(-1)(25-3x) \\ \\ 2y=3x-25 \\ \\ y=(3x-25)/(2) \end{gathered}`

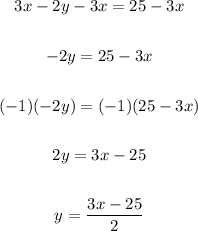
Now, we can replace y with the above expression in the second equation. We obtain:

`\begin{gathered} 5x+10\cdot(3x-25)/(2)=-25 \\ \\ 5x+(10)/(2)(3x-25)=-25 \\ \\ 5x+5(3x-25)=-25 \\ \\ 5x+15x-125=-25 \\ \\ 20x-125+125=-25+125 \\ \\ 20x=100 \\ \\ x=(100)/(20) \\ \\ x=5 \end{gathered}`

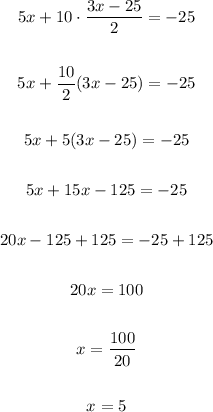
Now, we use x = 5 to find y:

`\begin{gathered} y=(3(5)-25)/(2) \\ \\ y=(15-25)/(2) \\ \\ y=-(10)/(2) \\ \\ y=-5 \end{gathered}`

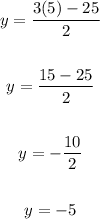
Therefore, the solution to this system is the ordered pair (5, -5).