In order to complete the square remember that
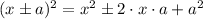
first, equal the expression divide all the expressions by 2,
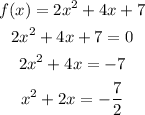
then, we can find "a" using the second portion of the definition
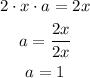
then,
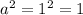
add 1 on both sides

rewrite as a square expression on the left,
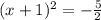
multiply both sides by 2

bring all to the left side and equal to f(x)
