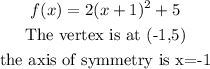Question

And also state the vertex and the axis of symmetry. I need help with number 2

Answer 1

In order to complete the square remember that

`(x\pm a)^2=x^2\pm2\cdot x\cdot a+a^2`

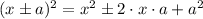
first, equal the expression divide all the expressions by 2,

`\begin{gathered} f(x)=2x^2+4x+7 \\ 2x^2+4x+7=0 \\ 2x^2+4x=-7 \\ x^2+2x=-(7)/(2) \end{gathered}`

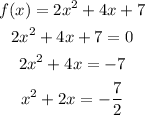
then, we can find "a" using the second portion of the definition

`\begin{gathered} 2\cdot x\cdot a=2x \\ a=(2x)/(2x) \\ a=1 \end{gathered}`

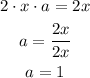
then,

`a^2=1^2=1`

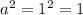
add 1 on both sides

`\begin{gathered} x^2+2x+1=-(7)/(2)+1 \\ x^2+2x+1=-(5)/(2) \end{gathered}`

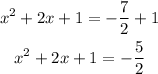
rewrite as a square expression on the left,

`(x+1)^2=-(5)/(2)`

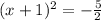
multiply both sides by 2

`2(x+1)^2=-5`

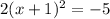
bring all to the left side and equal to f(x)

`\begin{gathered} f(x)=2(x+1)^2+5 \\ \text{The vertex is at (-1,5)} \\ \text{the axis of symmetry is x=-1} \end{gathered}`