Question

The population of a fish farm is modeled by the equation where t is time in yearsP(t) = 1250/ 2+3e ^ -0.6tpart one)part two)part three)part four)part five)

Answer 1

The Solution:

Given the equation that modeled the population of fish after time (t) in years as below:

`p(t)=(1250)/(2+3e^(-0.6t))`

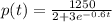
part 1:

We are to find the initial population of fish. This means we are to find the value of p when t = 0.

`p(0)=(1250)/(2+3e^(-0.6(0)))=(1250)/(2+3e^0)=(1250)/(2+3)=(1250)/(5)=250\text{ fish}`

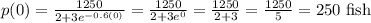
Part 2:

We are required to find the doubling time (t) for this population (Round the answer to the nearest tenth). This means we are to find t when P(t) = 500.

Note: double of 250 fish is 2x250 = 500 fish.

`\begin{gathered} p(t)=(1250)/(2+3e^(-0.6t)) \\ \\ \text{Where P(t)=500, and t=?} \end{gathered}`

`\begin{gathered} 500=(1250)/(2+3e^(-0.6t)) \\ \text{Cross multiplying, we get} \\ \\ 500(2+3e^(-0.6t))=1250 \\ \text{ Dividing both sides by 500, we get} \\ \\ (500(2+3e^(-0.6t)))/(500)=(1250)/(500) \end{gathered}`

`\begin{gathered} 2+3e^(-0.6t)=2.5 \\ \text{ Collecting the like terms, we get} \\ 3e^(-0.6t)=2.5-2 \\ 3e^(-0.6t)=0.5 \end{gathered}`

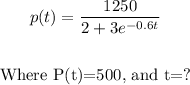
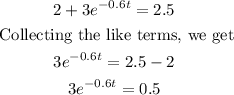
Dividing both sides by 3, we get

`\begin{gathered} (3e)/(3)^(-0.6t)=(0.5)/(3) \\ \\ e^(-0.6t)=(1)/(6) \end{gathered}`

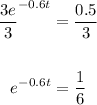
Taking the natural log of both sides, we get