The Solution:
Given the equation that modeled the population of fish after time (t) in years as below:

part 1:
We are to find the initial population of fish. This means we are to find the value of p when t = 0.
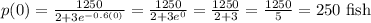
Part 2:
We are required to find the doubling time (t) for this population (Round the answer to the nearest tenth). This means we are to find t when P(t) = 500.
Note: double of 250 fish is 2x250 = 500 fish.


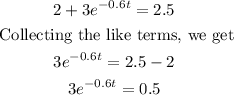
Dividing both sides by 3, we get
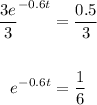
Taking the natural log of both sides, we get
![undefined]()