Question

A rectangular field is six times as long as it is wide. If the perimeter of the field is 1050 feet, what arethe dimensions of the field?A) Write an equation you can use to answer the given question. Let w be the width of the field. Donot solve the equation yet.The equation isB) Use your equation to find the dimensions of the field.The width of the field isThe length of the field is(Make sure you use the correct variable.)feet.feet.

Answer 1

Let

l be the length of the rectangular field

w be the width of the rectangular field

The rectangular field is 6 times as long as it is wide. This means that

`6w=l\text{ \lparen from the phrase ''six times as long as it is wide''\rparen}`

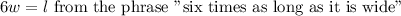
Part A:

Using the formula of the perimeter we have the following:

`\begin{gathered} 2l+2w=1050\text{ ft} \\ 2(6w)+2w=1050\text{ ft} \\ 12w+2w=1050\text{ ft} \\ 14w=1050\text{ ft} \end{gathered}`

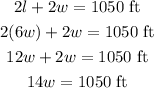
Part B:

Solve for width, and we get

`\begin{gathered} 14w=1050\text{ ft} \\ (14w)/(14)=\frac{1050\text{ ft}}{14} \\ w=75\text{ ft} \\ \\ \text{Therefore, the width of the field is }75\text{ ft}. \end{gathered}`

Substitute the width back to the formula to solve for the length

`\begin{gathered} 2l+2w=1050\text{ ft} \\ 2l+2(75\text{ ft})=1050\text{ ft} \\ 2l+150\text{ ft}=1050\text{ ft} \\ 2l=1050\text{ ft}-150\text{ ft} \\ 2l=900\text{ ft} \\ (2l)/(2)=\frac{900\text{ ft}}{2} \\ l=450\text{ ft} \\ \\ \text{Therefore, the length of the field is }450\text{ ft}. \\ \end{gathered}`