Let
l be the length of the rectangular field
w be the width of the rectangular field
The rectangular field is 6 times as long as it is wide. This means that
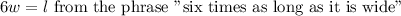
Part A:
Using the formula of the perimeter we have the following:
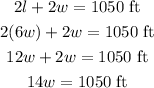
Part B:
Solve for width, and we get

Substitute the width back to the formula to solve for the length
