Question

Hello, I need help solving this problem. Thank you so much

Answer 1

`(x)/(x+4)+(3)/(x+5)=(x+2)/(x^2+9x+20)`

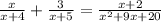
1. Factor the denominator of the expression on the irhgt of the equation:

- Write 9x as the sum of two terms that when you muliply the coefficient the result is 20:

`x^2+9x+20=x^2+5x+4x+20`

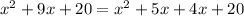
-Factor by parts: (common factor in frist two terms x and common factor in last two terms 4)

`=x(x+5)+4(x+5)`

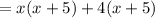
-Factor (x+5)

`=(x+5)(x+4)`

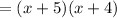
Then, the given equation after the frist step is:

`(x)/(x+4)+(3)/(x+5)=(x+2)/((x+5)(x+4))`

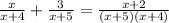
2. Subtract the fraction on the right in both sides of the equation:

`\begin{gathered} (x)/(x+4)+(3)/(x+5)-(x+2)/((x+5)(x+4))=(x+2)/((x+5)(x+4))-(x+2)/((x+5)(x+4)) \\ \\ (x)/(x+4)+(3)/(x+5)-(x+2)/((x+5)(x+4))=0 \end{gathered}`

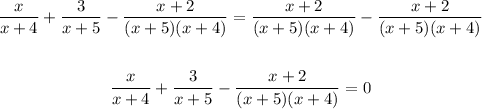
3. Write each fraction with LCD (x+5)(x+4)

-First fraction: multiply numerator and denominator by (x+5):

`(x)/(x+4)\cdot(x+5)/(x+5)=(x(x+5))/((x+5)(x+4))`

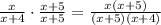
-Second fraction: multiply numerator and denominator by (x+4)

`(3)/(x+5)\cdot(x+4)/(x+4)=(3(x+4))/((x+5)(x+4))`

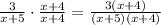
-Third fraction is written with the LCD.

Then, the expression written with LCD is:

`(x(x+5))/((x+5)(x+4))+(3(x+4))/((x+5)(x+4))-(x+2)/((x+5)(x+4))=0`

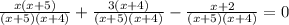
4. Solve the operartions of the fractions:

`(x(x+5)+3(x+4)-(x+2))/((x+5)(x+4))=0`

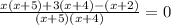
Simplify:

`\begin{gathered} (x^2+5x+3x+12-x-2)/((x+5)(x+4))=0 \\ \\ (x^2+7x+10)/((x+5)(x+4))=0 \end{gathered}`

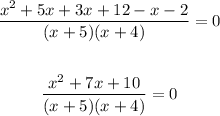
5. Factor the numerator:

-Write 7x as the sum of two terms that when you muliply the coefficient the result is 10:

`x^2+7x+10=x^2+5x+2x+10`

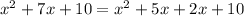
-Factor by parts: (comon term in frist two terms is x, and comon factor in last two temrs is 2):

`=x(x+5)+2(x+5)`

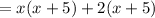
-Factor (x+5):

`=(x+5)(x+2)`

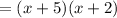
Then, the equation after this step is:

`((x+5)(x+2))/((x+5)(x+4))=0`

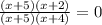
6. Simplify:

`(x+2)/(x+4)=0`

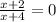
7. Solve x:

When the quotient (result of division) is equal to 0, the numerator is equal to 0:

`\begin{gathered} x+2=0 \\ \\ \text{Subtract 2 in both sides of the equation:} \\ x+2-2=0-2 \\ x=-2 \end{gathered}`

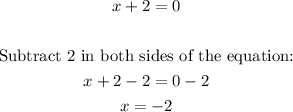
Then, the solution for the given eqution is: x= -2