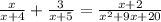
1. Factor the denominator of the expression on the irhgt of the equation:
- Write 9x as the sum of two terms that when you muliply the coefficient the result is 20:
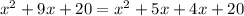
-Factor by parts: (common factor in frist two terms x and common factor in last two terms 4)
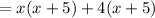
-Factor (x+5)
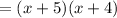
Then, the given equation after the frist step is:

2. Subtract the fraction on the right in both sides of the equation:
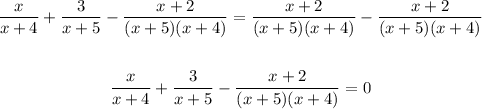
3. Write each fraction with LCD (x+5)(x+4)
-First fraction: multiply numerator and denominator by (x+5):
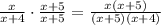
-Second fraction: multiply numerator and denominator by (x+4)
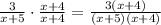
-Third fraction is written with the LCD.
Then, the expression written with LCD is:
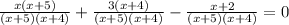
4. Solve the operartions of the fractions:
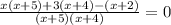
Simplify:
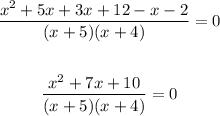
5. Factor the numerator:
-Write 7x as the sum of two terms that when you muliply the coefficient the result is 10:

-Factor by parts: (comon term in frist two terms is x, and comon factor in last two temrs is 2):
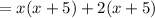
-Factor (x+5):
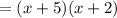
Then, the equation after this step is:
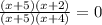
6. Simplify:
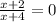
7. Solve x:
When the quotient (result of division) is equal to 0, the numerator is equal to 0:

Then, the solution for the given eqution is: x= -2