We will investigate how to determine Hamilton paths and circuits
Hamilton path: A path that connect each vertex/point once without repetition of a point/vertex. However, the starting and ending point/vertex can be different.
Hamilton circuit: A path that connect each vertex/point once without repetition of a point/vertex. However, the starting and ending point/vertex must be the same!
As the starting point we can choose any of the points. We will choose point ( F ) and trace a path as follows:
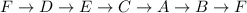
The above path covers all the vertices/points with the starting and ending point/vertex to be ( F ). Such a path is called a Hamilton circuit per definition.
We will choose a different point now. Lets choose ( E ) as our starting point and trace the path as follows:
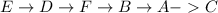
The above path covers all the vertices/points with the starting and ending point/vertex are different with be ( E ) and ( C ), respectively. Such a path is called a Hamilton path per definition.
One more thing to note is that all Hamilton circuits can be converted into a Hamilton path like follows:
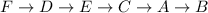
The above path is a hamilton path that can be formed from the Hamilton circuit example.
But its not necessary for all Hamilton paths to form a Hamilton circuit! Unfortunately, this is not the case in the network given. Every point is in a closed loop i.e there is no loose end/vertex that is not connected by any other vertex.