We have a geometric sequence, with a(2) = 5 and r = -2.
We can write geometric sequences in general as:
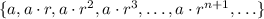
So we can write the second term, a(2), as:
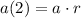
As we know a(2) and r, we can calculate the base "a" as:
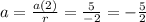
Any term can be calculated as:
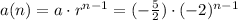
Then, the eight term a(8) can be then calculated as:
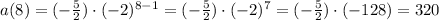
Answer: a(8) = 320