Question

Solve #3 and explain to me the steps to solve it.

Answer 1

the solution works in both equations

See graph below

Step-by-step explanation:
`\begin{gathered} 3)\text{ }y\text{ =-}(1)/(2)x\text{ + 3} \\ \text{ }y\text{ = 5} \end{gathered}`

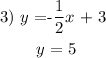
To plot y = 5, it will be an horizontal line on y = 5 that extends towards the negative and positive side of the graph

y = -1/2 x + 3

This is a linear equation. To plot this graph, we will assign values to x in order to get corresponding values to y

let x = -5, 0 5

when x = -5

y = -1/2 (-5) + 3 = 5/2 + 3

y = 5 1/2

when x = 0

y = -1/2 (0) + 3 = 0 + 3

y = 3

when x = 5

y = -1/2 (5) + 3 = -5/2 + 3

y = -1/2

plotting the graph:

The point of intersection is the solution of the graph. The point of intersection is (-4, 5)

x = -4, y = 5

To check if the solution is correct, we will substitute 5 for y in the first equation since the value of y from our solution is 5

y = -1/2 x + 3

5 = -1/2 (-4) + 3

5 = 2 + 3

5 = 5

Since the left and side is equal to right hand side, it is true

We can also test for x

when x = -4

y = -1/2 (-4) + 3

y = 4/2 + 3

y = 2 + 3

y = 5

This is the same value as y in our solution using graph

Hence, the solution works in both equations