Question

Prove the identity.(cot²x+1) (sin ²x-1)=-cot²x

Answer 1

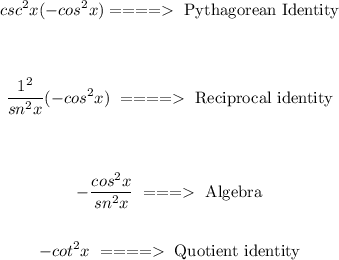
Given:

`(cot^2x+1)(sin^2x-1)=-cotx`

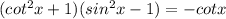
Let's verify the identity.

Apply Pythagorean identity on the left:

`\begin{gathered} (1+cos^2x)(-1+sin^2x)=-cotx \\ \\ csc^2x(-cos^2x)=-cotx \end{gathered}`

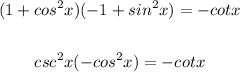
The next step is to apply reciprocal identity.

`\begin{gathered} \text{ Where:} \\ csc^2x=((1)/(sinx))^2 \end{gathered}`

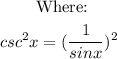
Thus, we have:

`\begin{gathered} ((1)/(sinx))^2(-cos^2x)=-cotx \\ \\ (1^2)/(sin^2x)(-cos^2x)=-cotx \end{gathered}`

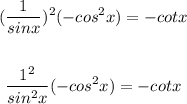
Solving further:

`(-cos^2x)/(sin^2x)=-cotx`

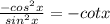
Apply quotient identity:

`\begin{gathered} \text{ Where:} \\ cotx=(cosx)/(sinx) \end{gathered}`

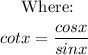
Using the quotient identity, we have:

`-(cos^2x)/(sin^2x)=-cot^2x`

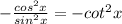
Therefore, the given equation is an identity.

We have the following:

`\begin{gathered} csc^2x(-cos^2x)====>\text{ Pythagorean Identity} \\ \\ \\ (1^(2))/(s\imaginaryI n^(2)x)(-cos^2x)\text{ }====>\text{ Reciprocal identity} \\ \\ \\ -(cos^2x)/(s\imaginaryI n^2x)\text{ }===>\text{ Algebra} \\ \\ -cot^2x\text{ }====>\text{ Quotient identity} \end{gathered}`