Question

Solve each system of linear equations by substitutionx+y=3-4x - 4y=12

Answer 1

We are given the following two equations

`\begin{gathered} x+y=3\qquad eq.1 \\ -4x-4y=12\qquad eq.2 \end{gathered}`

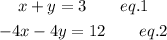
Let us solve this system of equations using the substitution method.

From eq. 1, sperate the variable x or y then substitute it into eq. 2

`x=3-y\qquad eq.1`

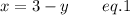
Now substitute it into eq. 2

`\begin{gathered} -4x-4y=12 \\ -4(3-y)-4y=12 \\ -12+4y-4y=12 \\ -12=12 \end{gathered}`

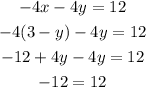
As you can see, the y variable canceled out and the equation became -12 = 12 which is not correct.

This means that there is no solution for this system of equations.

These equations are parallel and do not intersect at any point and it can be confirmed by looking at the graph of these equations.

Therefore, the given system of equations has no solution.