Given data:
Mass of the person;
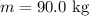
Mass of the planet;
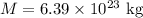
Radius of the planet;
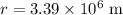
The gravitational force is given as,
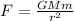
Here, is universal gravitational constant.
Substituting all known values,
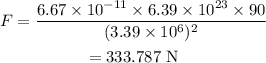
Therefore, the gravitational force experinced by the person is 333.787 N.