Question

Find the area between the curves y = e ^ (- 0.7x) and y = 2.3x + 1 from x = 0 to x = 4

Answer 1

The area between the curves is given by:

`A=\int_a^b[|f(x)-g(x)|]dx`

Where a=0 and b=4.

And

`\begin{gathered} f(x)=e^(-0.7x) \\ g(x)=2.3x+1 \end{gathered}`

Replacing.

`A=\int_0^4(e^(-0.7x)-(2.3x+1))dx`

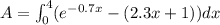
Solving:

`A=\int_0^4e^(-0.7x)dx-\int_0^42.3xdx-\int_0^41dx`
`A=(e^(-0.7z))/(-0.7)-2.3*(x^2)/(2)-x`

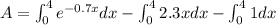
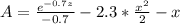
Replacing x by the limits:

`A=((e^(-0.7*4))/(-0.7)-(e^(-0.7*0))/(-0.7))-(2.3)/(2)(4^2-0^2)-(4-0)`
`\begin{gathered} A=(1)/(-0.7)(-0.939)-(2.3)/(2)(16)-4 \\ \\ A=(1)/(0.7)(0.939)-(2.3)/(1)(8)-4 \end{gathered}`

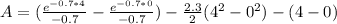
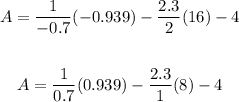
Therefore, the area is:

`A=-21.0585`

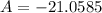
Taking the absolute value:

`A=|-21.0585|=21.0585`

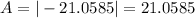
We take absolute value because negative areas make no sense.

Answer: The area between the curves is: 21.06 approximately 21.1.