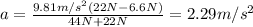ANSWER
2.29 m/s²
Step-by-step explanation
The free body diagram of this situation, when block C is lifted off A is
Now we know that blocks A and B are moving, so the equations according with Newton's second law of motion for each block are:
Block A:
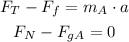
Block B (there are not horizontal forces):
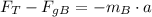
From the equation for block B, we have that the tension of the rope is:
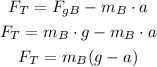
And mB is:
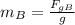
So the tension force is:
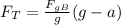
The kinetic friction force, when the coefficient of kinetic friction betwen the surfaces is μk is:
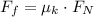
The normal force, from the second equation of block A is:
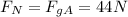
So the friction force between block A and the table is:
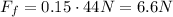
Now, using the first equation for block A, we can find its acceleration. But before doing that, we have to find the mass of block A - remember that we have the weight, not the mass. This we find with the equation of weight:
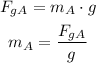
Replacing Ft, Ff and mA into the first equation of block A:

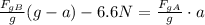
We have an equation which we can solve for a. Apply distributive property in the first term:

Then add the second term from both sides:
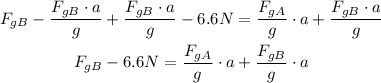
Take a as a common factor from the right side of the equation:

And then divide by the coefficient of a:
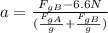
Since g is a common denominator we can simplify the expression a little before replacing with values:
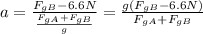
Now we can replace and find a: