Part A:
System of equations is a set of two or more equations involving the same set of variables and having the same solution.
Part B:
A problem can be solved using system of twoequations if two quantities are involved and there is a value associated with each quantity.
A problem that can be solved using the system of equations is given below.
The total number of boys and girls in a class is 40. Each boys has $1 with him and each girl has $2. The total amount the students in the class have is $65. Find the number of boys and girls in the class.
The number of boys and girls in the class can be found by creating two equations and solving it.
Part C:
Given:
The selling price of a sign, s=$20.
The selling price of a towel, t=$7.5.
The total money earned by selling signs and towels, T=$250.
Let x be the number of signs and y be the number of towels.
So, the expression for total money earned by selling signs and towels is,
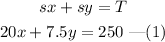
It is given that Lindsay sells as many Towels as signs.
So, we can write
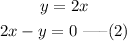
So, we obtained two equations in x and y.
Multiply equation (2) by 10.
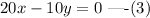
Subtract (3) from (1).
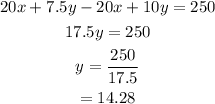
Putting y=14.28 in equation (1), we can find the value of x also.
Hence, the given problem can be solved using the system of equations.