Answer:
The equations are given below as
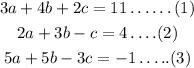
Step 1:
Multiply equation 1 by 2 and multiply equation 2 by 3
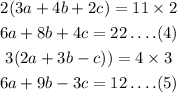
Step 2:
Substract equation 4 from 5
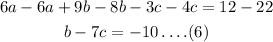
Step 3:
Multiply equation (2) by 5 and then equation 3 by 3
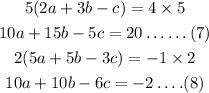
Step 4:
Substract equation (8) from equation (7)
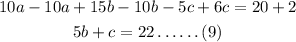
Step 5:
From equation (9)
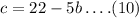
Substitute equation 10 in equation (6)
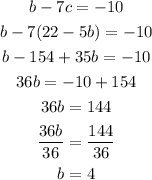
Step 6:
Substitute the value of b=4 in equation (10)
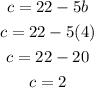
Step 7:
Substitute c=2 and b=4 in equation (2)
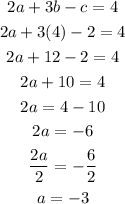
Hence,
a =-3 , b=4 , c=2
OPTION C is the right answer