ANSWER

Step-by-step explanation
The vertex form of a quadratic equation is:

where (h, k) = vertex
Let us substitute the given vertex and the given point into the equation to find the value of the constant a.
That is:

That is the value of the constant a. Now we can write the quadratic function using the constant a and the vertex:
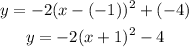
That is the function.