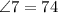Question

The figure to the right shows two parallel lines intersected by a transversal.Let x = 106° Find the measure of each of the other seven angles.

Answer 1

Angles of the first line are the same of the second line because the lines are parallel and intersected by the same line

then

`\begin{gathered} x=\angle4 \\ 1=\angle5 \\ 2=\angle6 \\ 3=\angle7 \end{gathered}`

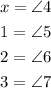
then

`\angle4=106`

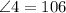
Now the opposite angles by the vertex like X and angle2 have the same value

then

`\angle2=106`

and

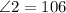
`\angle6=106`

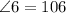
the adjacent angle of each angle make a straight angle then the sum is 180

now if we sum x and angle 1 we have 180

`x+\angle1=180`

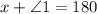
we replace the value of x and solve for angle 1

`\begin{gathered} 106+\angle1=180 \\ \angle1=180-106 \\ \angle1=74 \end{gathered}`

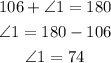
opposite angle by the vertex of angle1 is angle3, then

`\angle3=74`

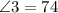
and angle3 and 7 are the same

`\angle7=74`