Answer:
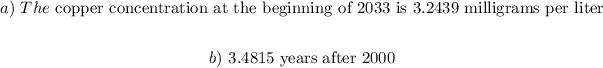
Step-by-step explanation:
Given:
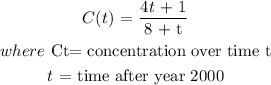
To find:
a) the copper concentration at the beginning of the year 2033
b) the time the maximum contaminate level of 1.3 m/L will be reached
a) year 2033 = 2000 + 33
since t is the time after year 2000
t = 33
To get the copper concentration, we will substitute for t in the formula:

b) To get the time it takes to get to the maximum contaminate level of 1.3 mg/l, we will substitute 1.3 for C(t) in the function:
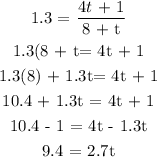
divide both sides by 2.7:
