The probablity that first one selected is a criminal justice major is,
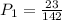
Now, the probablity that second one is a criminal justice major is when selected without replacement,
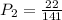
Simirally,
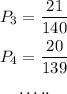
Thus, using the multiplication theorem,
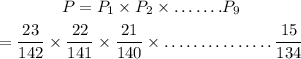
Thus, the above equation gives the requried probablity.