The sum of the interior angles of a triangle must be 180 degrees, so the angle C in the triangle ACE must be
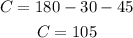
We see that the other angles that share the vertex with C are opposed by the vertex, so they must have the same measure, and, even more, they are supplementary with C, then these angles must be
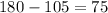
75 degrees. Now, we can obtain x and y

Then the sum is
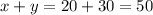
So, the answer is (B) 50