Question

Completely factor the trinomial, if possible.70u^4+115u^3+15u^2

Answer 1

5u²(7u+1)(2u+3).

Explanation:

Given the trinomial:

`70u^4+115u^3+15u^2`

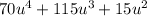
Each of the terms can be divided by 5 and u².

We first factor this out.

`\begin{gathered} 70u^4+115u^3+15u^2=5u^2((70u^4)/(5u^2)+(115u^3)/(5u^2)+(15u^2)/(5u^2)) \\ =5u^2(14u^2+23u+3) \end{gathered}`

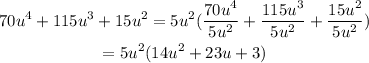
Next, we factor the quadratic trinomial inside the parentheses.

To factor the trinomial:

To find the two numbers, we need two terms:

• Whose sum is the middle term, 23u

,

• Whose product is: 3 x 14u² = 42u²

`\begin{gathered} 21u+2u=23u \\ (21u)(2u)=42u^2 \end{gathered}`

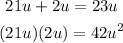
Replace the middle term with the sum.

`5u^2(14u^2+23u+3)=5u^2(14u^2+21u+2u+3)`

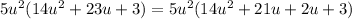
Finally, group and factor:

`\begin{gathered} =5u^2\lbrack7u(2u+3)+1(2u+3)\rbrack \\ =5u^2(7u+1)(2u+3) \end{gathered}`

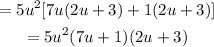
The factored form of the trinomial is 5u²(7u+1)(2u+3).