Answer:
5u²(7u+1)(2u+3).
Explanation:
Given the trinomial:

Each of the terms can be divided by 5 and u².
We first factor this out.
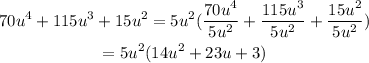
Next, we factor the quadratic trinomial inside the parentheses.
To factor the trinomial:
To find the two numbers, we need two terms:
• Whose sum is the middle term, 23u
,
• Whose product is: 3 x 14u² = 42u²
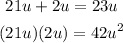
Replace the middle term with the sum.

Finally, group and factor:
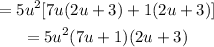
The factored form of the trinomial is 5u²(7u+1)(2u+3).