Question

Question: If A denotes the area of the sector of a circle of radius r formed by the central angle θ, find the missing quantity. θ= π/4 radians, A=84 squaremeters So r=?131.88m5.74m14.63m32.97m

Answer 1

Recall that the area of a sector of a circle of radius r formed by the central angle θ radians is:

`A=(\theta)/(2)r^2\text{.}`

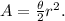
Substituting θ=π/4, and A=84m² we get:

`84m^2=((\pi)/(4))/(2)r^2\text{.}`

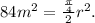
Simplifying the above result we get:

`84m^2=(\pi)/(8)r^2.`

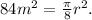
Multiplying the above equation by 8/π we get:

`\begin{gathered} 84m^2*(8)/(\pi)=(\pi)/(8)r^2*(8)/(\pi), \\ r^2=(672)/(\pi)m^2\text{.} \end{gathered}`

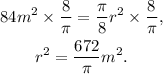
Therefore:

`\begin{gathered} r=\sqrt[]{(672)/(\pi)}m \\ \approx14.63m \end{gathered}`

Answer: Third option, 14.63m.