Question

Solve the system of equations by converting to a matrix equations and using inverse of the coefficient matrix.

Answer 1

`\begin{gathered} -2y+2z=12 \\ 3x+y+3z=-2 \\ x-2y+3z=8 \end{gathered}`

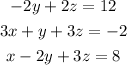
The matrix conversion of the above system of equation is:

`\begin{bmatrix}{0} & {-2} & {2} \\ {3} & {1} & {3} \\ {1} & {-2} & {3}\end{bmatrix}\begin{bmatrix}{x} & {} & {} \\ {y} & {} & {} \\ {z} & {} & {}\end{bmatrix}=\begin{bmatrix}{12} & {} & {} \\ {-2} & {} & {} \\ {8} & {} & {}\end{bmatrix}`

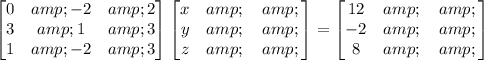
In this case:

a = 0, b = -2, c = 2

d = 3, e = 1, f = 3

g = 1, h = -2, i = 3

To solve this system of equation, we have to determine its determinant first. To solve the determinant of a 3x3 matrix, we have the formula below:

`\begin{gathered} \det =a(ei-fh)-b(di-fg)+c(dh-eg) \\ \det =0+2(3\cdot3-3\cdot1)+2(3\cdot-2-1\cdot1) \\ \det =0+2(9-3)+2(-6-1) \\ \det =0+2(6)+2(-7) \\ \det =12-14 \\ \det =-2 \end{gathered}`

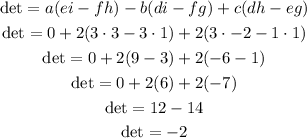
Therefore, the determinant is -2, and therefore, the inverse of this matrix can be solved.

The next thing to is do calculate the determinant of the 2x2 minor matrices.

Let's start with the first row elements.

`\begin{gathered} \begin{bmatrix}{1} & {3} & {} \\ {-2} & {3} & {} \\ {} & {} & {}\end{bmatrix}=3--6=9 \\ \begin{bmatrix}{3} & {3} & {} \\ {1} & {3} & {} \\ {} & {} & {}\end{bmatrix}=9-3=6 \\ \begin{bmatrix}{3} & {1} & {} \\ {1} & {-2} & {} \\ {} & {} & {}\end{bmatrix}=-6-1=-7 \end{gathered}`

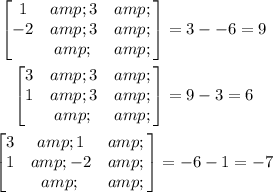
Let's move on to the second-row elements.

`\begin{gathered} \begin{bmatrix}{-2} & {2} & {} \\ {-2} & {3} & {} \\ {} & {} & {}\end{bmatrix}=-6--4=-2 \\ \begin{bmatrix}{0} & {2} & {} \\ {1} & {3} & {} \\ {} & {} & {}\end{bmatrix}=0-2=-2 \\ \begin{bmatrix}{0} & {-2} & {} \\ {1} & {-2} & {} \\ {} & {} & {}\end{bmatrix}=0+2=2 \end{gathered}`

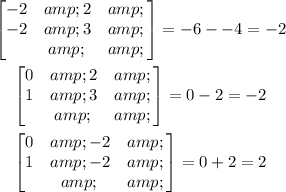
Lastly, for the third-row elements:

`\begin{gathered} \begin{bmatrix}{-2} & {2} & {} \\ {1} & {3} & {} \\ {} & {} & {}\end{bmatrix}=-6-2=-8 \\ \begin{bmatrix}{0} & {2} & {} \\ {3} & {3} & {} \\ {} & {} & {}\end{bmatrix}=0-6=-6 \\ \begin{bmatrix}{0} & {-2} & {} \\ {3} & {1} & {} \\ {} & {} & {}\end{bmatrix}=0+6=6 \end{gathered}`

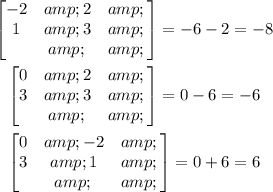
The new matrix formed is:

`\begin{bmatrix}{9} & {6} & {-7} \\ {-2} & {-2} & {2} \\ {-8} & {-6} & {6}\end{bmatrix}`

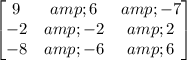
From the new matrix, let's form the matrix of cofactors by leaving alternating signs.

`\begin{bmatrix}{9} & {6} & {-7} \\ {-2} & {-2} & {2} \\ {-8} & {-6} & {6}\end{bmatrix}*\begin{bmatrix}{+} & {-} & {+} \\ {-} & {+} & {-} \\ {+} & {-} & {+}\end{bmatrix}=\begin{bmatrix}{9} & {-6} & {-7} \\ {2} & {-2} & {-2} \\ {-8} & {6} & {6}\end{bmatrix}`

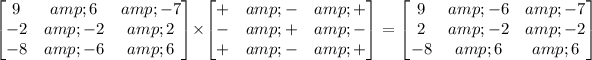
Now that we have the cofactor matrix, let's get the adjugate matrix by transposing the rows and columns. The adjugate matrix is:

`\begin{bmatrix}{9} & {2} & {-8} \\ {-6} & {-2} & {6} \\ {-7} & {-2} & {6}\end{bmatrix}`

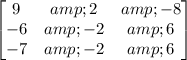
The next step is to multiply the adjugate matrix to 1/determinant to get the inverse of the 3x3 matrix. Recall that the determinant of the 3x3 matrix is -2.

`-(1)/(2)*\begin{bmatrix}{9} & {2} & {-8} \\ {-6} & {-2} & {6} \\ {-7} & {-2} & {6}\end{bmatrix}=\begin{bmatrix}{-(9)/(2)} & {-1} & {4} \\ {3} & {1} & {-3} \\ {(7)/(2)} & {1} & {-3}\end{bmatrix}`

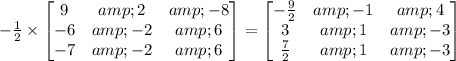
Now that we have the inverse of the 3x3 matrix, let's multiply this to the matrix [12 -2 8} to solve for x, y, z.

`\begin{bmatrix}{-(9)/(2)} & {-1} & {4} \\ {3} & {1} & {-3} \\ {(7)/(2)} & {1} & {-3}\end{bmatrix}*\begin{bmatrix}{12} & {} & {} \\ {-2} & {} & {} \\ {8} & {} & {}\end{bmatrix}=\begin{cases}x=-20 \\ y=10 \\ z=16\end{cases}`

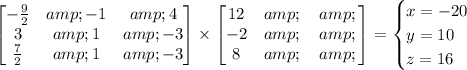
Therefore, x = -20, y = 10, and z = 16.

To check if this is right, let's substitute these values to the equations above.

`\begin{gathered} -2y+2z=12 \\ -2(10)+2(16)=12 \\ -20+32=12 \\ 12=12 \end{gathered}`
`\begin{gathered} 3x+y+3z=-2 \\ 3(-20)+10+3(16)=-2 \\ -60+10+48=-2 \\ -2=-2 \end{gathered}`
`\begin{gathered} x-2y+3z=8 \\ -20-2(10)+3(16)=8 \\ -20-20+48=8 \\ 8=8 \end{gathered}`

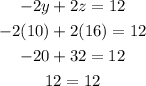
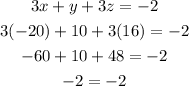
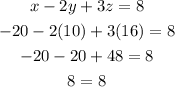
Indeed, x = -20, y = 10, and z = 16.